概率分布入门 1

What is a Probability Distribution?

Probability distributions allow you to represent the probability of an event using a mathematical equation. Like any mathematical equation:

probability distributions can be visualized using a graph especially in 2-dimensional cases.
probability distributions can be worked with using algebra, linear algebra and calculus.

These distributions make it much easier to understand and summarize the probability of a system whether that system be a coin flip experiment or the location of an autonomous vehicle.

概率分布入门 2

Types of Probability Distributions

Probability distributions are really helpful for understanding the probability of a system.
Looking at the big pictures, there are two types of probability distributions:

discrete probability distributions
continuous probability distributions

Before we get into the details about what discrete and continuous mean, take a look at these two visualizations below. The first image shows a discrete probability distribution and the second a continuous probability distribution. What is similar and what is different about each visualization?

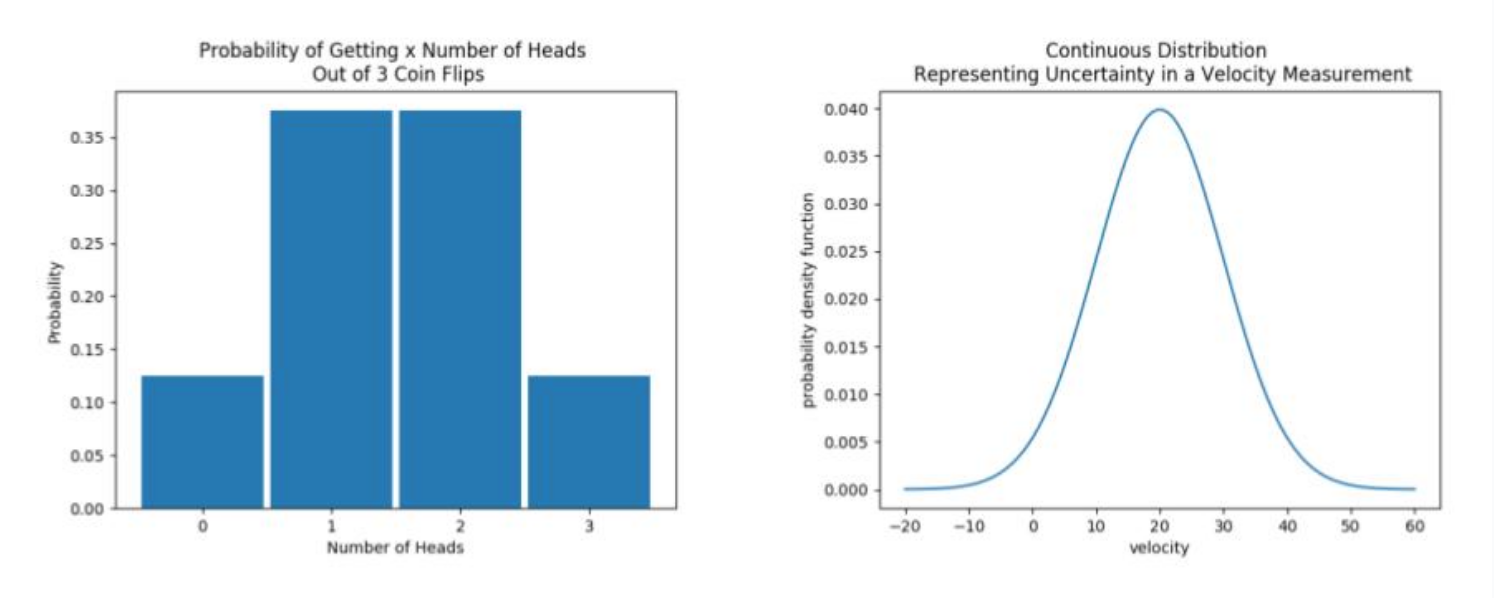
Discrete Distribution (left) and Continuous Distribution (right).

SOLUTION:

The x-axis represents the main variable/event of interest for both visualizations.
In the discrete visualization, the x-axis variable can only take on certain values such as 1, 2 or 3.
In the continuous visualization, the x-axis variable can take on any real number value from -infinity to +infinity.

More terminology

Prior - a prior probability distribution of an uncertain quantity, such as the location of a self-driving car on a road. This is the probability distribution that would express one's beliefs about the car's location **before ** some sensor measurements or other evidence is taken into account.
Posterior - the probability distribution of an uncertain quantity, after some evidence (like sensor measurements) have been taken into account.

And you'll learn more about this terminology in the upcoming videos!